Learning to Extract Local Events from the Web
Completed:
This paper, published by John Foley, Michael Bendersky and Vanja Josifovski, is about how to extract local events from the web, using techniques from the information retrieval theory.

Introduction
Now more than ever before, we are surrounded by recommendation engines. Those are used for any kind of activities of our every day life. However, to have a performant recommendation engine, it must have correct, trusted data to recommend. While big social medias or e-commerce websites can use their own data, it is however trickier if you want to collect data from scraping websites. The adoption of semantic web has grown over the years, making it easier for massive extraction of information using machine-readable annotations. However, there will always be organizations without the resources or the expertise to marking up pages with microdata like from the website schema.org. In this paper, researches focused on building an algorithm that can extract events from the web, like concert or sport competition, but also small local events (theater performances, garages sales, movie screening etc… ). Researchers showed that their algorithm learned to extract large events from well organized web pages, but also from smaller ones, using a technique of distant supervision to assign scores to individual events fields, and then a model that groups these fields into complete event records.
Event Extraction Model
First of all, what is an “event” ? Researchs gave a definition by those terms :
Definition : An event occurs at a certain location, has a start date and time, and a title and a description. In other words, to be useful to a user, an event must be able to answer the question : What ? When ? Where ?
To tackle the issue of retrieving many events from the web, we can see this problem as a scoring or ranking algorithm to train. This technique is divided in two parts :
- One model that joins several fields and give a score on how well those fields fits the model of an event.
- A grouping algorithm that provides an efficient way to optimize the quality of extracted event records.
We can represent an extracted event from a web page as set of fields $(\mathcal{F}={f_1,f_2,…,f_n})$, their enclosing region ($\mathcal{R}$) and the source domain ($\mathcal{D}$)
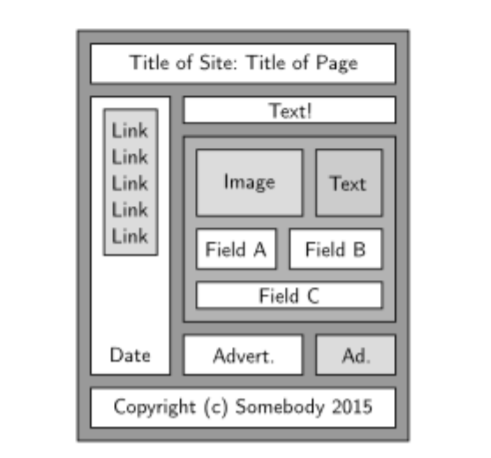
Example of an HTML document structure, presented visually. The boxes present represent nodes, the white boxes are the ones that are plausibly detected as fields in this example.Subsets of these fields represent possible event extractions.
In the figure above, if we consider this document being one event, it is likely that the fields A, B and C will contain the key information of the event. An event extraction only including the copyright should get a low score, and similarly one containing all the fields should be considered too big and also receive a low score.
We formulate our scoring function as follows :
\[\phi(\mathcal{F},\mathcal{R},\mathcal{D}) = \alpha(\mathcal{D})\beta(\mathcal{R})\gamma(\mathcal{F})\]We will discuss in detail each part of this function.
Document Scoring
Since we are treated many web pages, and most of them will not have any event in it, we want to have a probability of how likely this page is to contain an event. To this end, we take a Naive-Bayes approach, and define the event class $E$, where if a document $D \in E$, it means $D$ is an event-document. For a candidate document, we can denote the probability of it belonging to the event class by :
\[\frac{P(E|D)}{P(\bar{E}|D)}>1\]where $\bar{E}$ is the non-event class. We can estimate those probabilities based upon the commonly used language modelling framework, where the major assumption is that we can treat all of our terms as being independent. We can therefore estimate the probability of a whole document by the probability of all its component terms ($w\in \mathcal{D}$)
\[P(\mathcal{D} \in X) = \prod_{w \in \mathcal{D}}\frac{tf(w,X)}{tf(*,X)}\]where $X$ is either {$E, \bar E$}. Because our event class may be parse in comparison to any given document, we apply linear smoothing to our positive class to avoid zero probabilities.
\[P(E|D) = \prod_{w \in \mathcal{D}}\lambda P(w \in E) + (1-\lambda)P(w \in C)\]And because we approximate our non-event class by the language model of the entire collection, $\bar E = C$, we don’t need smoothing for this class.
\[P(\bar E |D) = \prod_{w \in \mathcal{D}}P(w \in C)\]Finally, since this algorithm will run on millions of pages, and we don’t to compute the other terms of our function $\phi$ , we choose to stop the calculation for a document for those whose $\alpha(\mathcal{D}) > 0$ , where $\alpha$ is defined as follows :
\[\alpha(\mathcal{D})=\left\{\begin{array}{ll} 1 & \log P(E | \mathcal{D})-\log P(\bar{E} | \mathcal{D})>0 \\ 0 & \text { otherwise } \end{array}\right.\]Now, we need to construct the model for the class E, a.k.a, regroup many pages of the event class to compute words probabilities. Researches scrapped 150,000 pages that had annotations from schema.org/Event. This allowed them to construct a robust event model.
Region Scoring
Now, we know if the document is susceptible to belong to the event class, great ! We need to focus our attention however on specific part of the document. This is the part where we look at the enclosing region $\mathcal{R}$. A region contains multiple fields. It is possibly then a good unstructured representation of the extracted event. Therefore, researchers simply decided to filter those regions according to their length :
\[\beta(\mathcal{R})=\left\{\begin{array}{ll} 1 & |\mathcal{R}|<\tau \\ 0 & \text { otherwise } \end{array}\right.\]where $\tau$ is set to $2^{12}$.
Field Set Scoring
This is the part where it gets more complex. We have 2/3 of the function, which leaves us with $\gamma (\mathcal{F})$. We want our set of fields $\mathcal{F} = (f_1,f_2,…f_n)$ to have at least on of the required field ( When, What, Where). This is done by separating $\gamma$ in a scoring function $\gamma_S$and an indicator function $\gamma_R$.
\[\gamma(\mathcal{F})=\left\{\begin{array}{ll} \gamma_{S}(\mathcal{F}) & \gamma_{R}(\mathcal{F}) \\ 0 & \text { otherwise } \end{array}\right.\]Score field function $\gamma_S$
The main task of this scoring function is to evaluate, for each $k \in ({What, Where, When})$, how likely is it to have the $k$ information in it. If you ever had to find postal code, adresse, or had to parse a date in a text, you know pattern-based approach can be very powerful. It is however much weaker for unstructured information, such as the $What$ field. In the following, researchers used this method as a baseline for their extraction of event on the $When$ and $Where$ fields, and assigned an equal score to all candidates for $What$.
No classification uses baseline approaches for all fields.
\[\begin{array}{l} \delta_{\text {What }}(f)=0.5 \\ \delta_{\text {Where }}(f)=\text { matches }(f, \text { Address }) \\ \delta_{\text {When }}(f)=\text { matches }(f, \text { Date } / \text { Time }) \end{array}\]What classification uses baseline approaches except for What fields.
\[\begin{array}{l} \delta_{\text {What }}(f)=\vec{W}_{\text {What }}^{T} \cdot \vec{X}_{f} \\ \delta_{\text {Where }}(f)=\text { matches }(f, \text { Address }) \\ \delta_{\text {When }}(f)=\text { matches }(f, \text { Date } / \text { Time }) \end{array}\]What-When-Where classification uses multiclass classification to rescore the boolean baseline approaches for all fields.
\[\begin{array}{l} \delta_{\text {What }}(f)=\vec{W}_{\text {What }}^{T} \cdot \vec{X}_{f} \\ \delta_{\text {Where }}(f)=\text { matches }(f, \text { Address }) \cdot \vec{W}_{\text {Where }}^{T} \cdot \vec{X}_{f} \\ \delta_{\text {When }}(f)=\text { matches }(f, \text { Date } / \text { Time }) \cdot \vec{W}_{\text {When }}^{T} \cdot \vec{X}_{f} \end{array}\]The patterned-based approach is implemented using the matches() function. The set of features $\vec{X}_{f}$ are extracted from the field and weights $\vec{W}_k$ are learned using LIBLINEAR. The features, without describing all of them, are Unigrams, Bigrams, ratio of terms capitalized, number of date field, location, number of adresses in the field etc. They then train a multiclassifier using those features and the web pages in the event class $E$. The label is set as : \(\mathcal{K}=\left[^{\prime} W h a t^{\prime},^{\prime} W h e n^{\prime},^{\prime} W h e r e^{\prime}, \text { 'Other }^{\prime}\right]\)
Using this classifier, we can now predict if a field is a What, a When or a Where field using the formulas : \(\text { PREDICTEDTYPE }(f)=\underset{k \in \mathcal{F}^{R}}{\operatorname{argmax}} \delta_{k}(f)\)
Improving the effiency
This field scoring algorithm can be very computational expensive if you need to score every fields of every documents as a ranking problem. To reduce the complexity, they only consider HTML tags that contain any baseline (regular expression pattern-based). This is however still not enough, so they added that a field can not be used twice, and use a greedy approach to be sure they do not miss the highest scoring events.
Finally, remember the formula for scoring a field in equation [1] ? $\alpha(\mathcal{D})$,$\beta(\mathcal{R})$ and $\gamma_{R}(\mathcal{F})$ are simple to calculate and may return zero scores, whereas $\left(\gamma_{S}(\mathcal{F})\right)$ is more computationnaly expensive. They decided to first compute those simple terms, and if any of them them is zero, skip the last field calculation.
Results
To test their method, researchers first thought of using the Schema.org dataset. However, all of theirs methods performed well, probably because of how well the data is structured. They decided to take the top 30,000 pages according to their document scoring $\alpha(\mathcal{D})$ and ran their algorithm three times, each pass with a different method of classification ($\textit{No baseline, What baseline, and the multiclass classification}$). Here is the result :
| None | What | What-Where-When | |
|---|---|---|---|
| Event | 0.54 | 0.51 | 0.76 |
| What | 0.09 | 0.30 | 0.36 |
| When | 0.17 | 0.20 | 0.32 |
| Where | 0.32 | 0.32 | 0.66 |
We can see that their method using the multiclass classifier outperforms the other techniques.
Conclusion
With this work, researchers have presented a new way a retrieving and recommend events. If it does not show a great improvement in large website with well structured data, it is however much more efficient for detecting local events on the open internet. Database like Schema.org was key in this work in order to train a robust classifier for the fields on event data. As more companies will start using such technologies, the more performant their extraction techniques will be.